Linear Circuit Analysis:
Steady State Power

We know how to find power with non-complex sources and elements. When complex sources and elements are involved the formulas for power are enhanced to compensate. Capacitors and inductors are referred to as lossless elements. Therefore, we say that they absorb no power. For complex sources, the formula that relates power to current and voltage is:

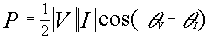
Given the voltage and a resistive element, the power absorbed by the resistor is given by the relationship:

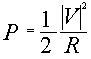• Call the cZeros function on the TI-92 by pressing [F2] [A] [3]. Enter the KCL equation assumed to be equal to zero. Store this to the variable v1.
  Note. Since the zeros and cZeros functions return their answers in the form of a list, the extra [1] parameter was used to extract the first (and in this case the only) element from the list before storing the complex number to v1.
• Press [2nd] [CUSTOM] to call the custom menu. Use the DegAng function by pressing [F3] [ENTER] [ENTER].

Now that we know the voltage we can find the power consumed by the resistor and the current source.

• Following the format of the equation in the text editor involving voltage and resistance, we find the power delivered to the resistor.
• Following the format of the equation in the text editor involving voltage and current, we find the power provided from the current source.
• The current through the branch I₂ is equal to the voltage at the top of I₂ (v1) divided by the resistance. Knowing that we can find this value we can easily solve for the current I₃ by KCL.
  I₃ = I_CS - I₂
• Store this answer in the variable i3.

• Knowing the current I₃ and the voltage provided by the voltage source, we can find the power absorbed by the voltage source. For this we use the formula for power involving complex current and complex voltage.

Given the circuit, find the value for Z_L for maximum average power transfer. Also find the value of the maximum average power transfer delivered to the load.
Irwin. page 468 example 10.6

• We find the open circuit voltage by multiplying the current through the 4 ohm resistor by the 4 ohm resistor. This value is stored to the variable v for later calculation.
• With the custom menu in place, press [F3] [ENTER] [ENTER] to change the complex number to a magnitude and an angle.

• Using the parallel function, we find the Thévenin impedance.
• The complex conjugate of the Thévenin impedance gives us the impedance for maximum average power transfer. Store this value in the variable z for later calculations.
• With the impedance given as before, we can calculate the current through the load. The current is calculated as the open circuit voltage divided by the total impedance (Z_th + Z_L). Since Z_th = conj(Z_L), the total impedance can be written as 2 * real(z). Store this value to the variable i for later calculations.
• With the custom menu in place, press [F3] [ENTER] [ENTER] to change the complex number to a magnitude and an angle.

• Now that we know the load impedance and the current through the load, we can use the formula given earlier that relates these two items to power.

• Store 6 as the value of the period to the variable t.
• Enter the text editor by pressing [APPS] [9] [ENTER], place the cursor on the formula for RMS value and press [F4] (Execute).
• After the problem has been evaluated, press [2nd] [QUIT] to return to the home screen.
• The value on the home screen is the RMS value for the current. To find the RMS value for the power delivered to the resistor delivered to a 4 ohm resistor, we need to apply the P=I²R formula

The current i(t) is flowing through a 4 ohm resistor. Determine the power absorbed by the resistor if:
i(t)=4sin(377t-30^o)+6cos(377t-45^o)A
Irwin. page 475 drill 10.10

Since the frequencies vary between the cosine and sine function, this problem needs to be done in two parts by way of superposition.

• Store the first part of the equation in the y(x) editor as y1(x).
• Store the second part of the equation in the y(x) editor as y2(x).

• Omega for the first part of this function is 377. Store the value of 2*Pi/377 to the variable t (Period).
• Press [APPS] [9] [ENTER] to go to the text editor. With the cursor on the line with the formula for RMS values, press [F4] (Execute).
• After the equation has been evaluated, press [2nd] [QUIT] to return to the home screen.
• The value on the home screen is the RMS value for the current. To find the RMS value for the power delivered to the 4 ohm resistor from the first part of the current source, we need to apply the P=I²R formula to find its contribution to the power. Store this in the variable named p1.

• Omega for the second part of this function is 754. Store the value of 2*Pi/754. to the variable t (Period).
• Scroll up to the equation for RMS value. Press [ENTER] to move it to the entry line. Change y1(x) to y2(x) and press [ENTER].
• The value on the home screen is the RMS value for the current. To find the RMS value for the power delivered to the 4 ohm resistor from the second part of the current source, we need to apply the P=I²R formula to find its contribution to the power. Store this in the variable named p2.
• Add p1 and p2 together to find the total power delivered to the resistor.
• Graph of y1(x), y2(x) and y3(x)=y1(x)+y2(x). xMax is set to 8*Pi/754 to show how the frequency of the current repeats.