Linear Circuit Analysis:

Charge and Current

Work, Power, Voltage, and
Resistance

Kirchoff's Laws

Y Delta, Node, and Loop

Circuits with Operational
Amplifiers

Network Theorems

Analysis of Diode Circuits

Capacitance and Inductance

First-Order Transient Circuits

AC Steady State Analysis

Steady State Power

The Power Factor

Introduction

adv.92g
circuits.92g
delta2yt.92g

Linear Circuit Analysis:
Circuits with Operational Amplifiers

Determine the gain for the circuit.
Irwin. page 142 example 3.25

The gain for all of the circuits containing Op-amps will be defined to be:

For our purposes, all op-amps will be considered to be ideal. Op-amps will be connected into the circuits around them at 4 different places.

Op-amps are modeled as small circuit segments. Therefore they can be drawn as:

With the model inserted into the network we obtain the following circuit. Notice the node connections and how they match up throughout all of the diagrams. Now that we have this circuit model, this problem can be solved by nodal analysis. The node equations, by KCL are:
At node V₁

At node V_out

These equations are written as the sum of all currents leaving the node equals 0.

Finding the coefficients of V₁ and V_out can prove to be non-trivial exercises in algebra. So, I have written a function entitled gcoef that is available in circuits.92g. There are two parameters passed into this function. The expression, assumed to be equal to zero, and the list of variables for which you want the coefficients. A list is returned with the first element being the coefficient of the first variable. The second element is the coefficient of the second variable. The last element in the returned list is scalar quantity that we will make the column vector with when we apply these elements to matrices.

We could take the time to put these expressions into their respective matrices and then perform the same linear algebra that we have been doing in the past examples, or we could use another function that I have written to do just this. The simul function, which is available in circuits.92g, also takes two parameters. The expression, assumed to be equal to zero, and the list of variables for which you want the coefficients. This function returns a column vector of equations showing what each of your variables is equal to.

These equations may still seem complex. However, one of the nice things about assuming that we are using ideal op-amps is that they have an infinite gain. The gain of the op-amp is represented in the schematics and the equations as a. So if we take the limit of the expression as a goes to infinity, we find the expressions greatly reduce.
What the problem called for was the gain of the network containing the op-amp. The gain was defined to be:

For our example V_out is represented by vo and V_in is represented by vs. This is true for both the schematics and the TI-92 screen shots. To find the gain of the network all we have to do is divide both sides of the equation by vs.
From this example we see that the output of an op-amp can be the input multiplied by a ratio of resistors.

To make these functions easier to access let's add them to the custom menu.

Then by entering cust() on the entry line, pressing [ENTER] [2nd] [CUSTOM] we can activate the new custom menu.

Determine an expression for the output voltage of the op-amp circuit.
Irwin. page 145 example 3.26

Another useful technique for solving circuits with ideal op-amps is to let the currents going into the op-amp equal zero, and to let the voltage at V₊ = the voltage at V_-.

The KCL node equation at the inverting terminal is:

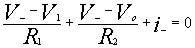
This equation is written as the sum of all the currents leaving the node equals zero.

At the non inverting terminal the KCL node equation yields:

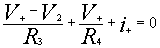
This equation is written as the sum of all the currents leaving the node equals zero.
On the TI-92, V₊is written as vp, V- is written as vm, i₊ is written as ip, and i- is written as im.

With ideal op-amps:
V₊ = V- = V
i₊ = i- = 0.

Now we can use the simul function to solve these KCL equations for V and V_o.

Note that if we let R₄ = R₂, and R₃ = R₁ the equation reduces.

Therefore, this circuit configuration can be used to subtract two input voltages.

Find the voltage gain of the op-amp circuit.
Irwin. page 167 prob 3.64

By letting V- = V₊ =V and i- = i₊ = 0, the KCL equations at the non inverting and inverting terminals are:

These KCL equations are written as the sum of the currents leaving the nodes equals zero.

Enter the KCL equation for the non inverting terminal of the op-amp and store in the variable named ninv.
Enter the KCL equation for the inverting terminal of the op-amp and store in the variable named inv.

Using the simul function, pass in the equations for the inverting and non inverting terminals as a list.
Solve for the voltages at V and V_o.

Divide the equations by V₁ and enter the values for the resistors.
R₁ = 20 ohms.
R₂ = 80 ohms.
R₃ = 1 ohm.
R₄ = 24 ohms.

From this we see that the gain equals 20 V/V.

For the circuit shown, find the gain.
DeCarlo. page 85 prob 3.10

The first node equation to recognize is the non inverting terminal of the first op-amp.

With this in mind along with V- = V₊ =V and i- = i₊ = 0, the KCL equation for the inverting terminal of the first op-amp is:

The KCL equation for the non inverting terminal of the second op-amp is:

And the KCL equation for the inverting terminal of the second op-amp is:

All of the KCL equations are written as the sum of the currents leaving the node equals zero.

Store the KCL equation for the inverting terminal of the first op-amp as inv1.
Store the KCL equation for the non inverting terminal of the second op-amp as ninv.
Store the KCL equation for the inverting terminal of the second op-amp as inv.

Using the simul function, pass in the equations for the inverting and non inverting terminals as a list.
Solve for the voltages at V2, V1o, and V_o.

Dividing this equation by V_s will show that the gain is equal to 3.2 V/V .

For the circuit, find the gain and plot the output for the given input voltage.
DeCarlo. page 84 prob 3.6

The gain is found by solving the KCL equations at the input terminals of the op-amp.
For the non inverting terminal the KCL equation is:

And the KCL equation for the inverting terminal is:

These equations are written as the sum of the currents leaving the node equals zero.
The graph was defined using the pcewise program available in circuits.92g.

Since V equals zero there is only one equation and one unknown. We can solve this equation using the built in solve function.
Divide the equation by V_S to find the gain.
The Pcewise program stored the graph of V_S in y1(x). Defining y2(x) to be the gain times y1(x) will allow us to see both graphs.

The graph shows the output of the op-amp is inverted with respect to the input. Also the magnitude is increased 5 times. Since most op-amps operate on a range of -15Volts < V_Out < +15Volts, this graph shows how the output is limited by the range of the op-amp.

There are more examples of Op-Amp circuits located at the bottom of the Capacitance and Inductance page.

Linear Circuit Analysis: Circuits with Operational Amplifiers

Linear Circuit Analysis:
Circuits with Operational Amplifiers