|
Plot the waveform for Vo of the
circuit.
DeCarlo. page 180 prob
6.8
For the branches containing the diodes, no current flows unless
Vs provides more voltage than the batteries underneath
the diodes. Therefore these branches are open circuits for
4.5V < Vs < 5.5V.
The equation for
the output voltage is:
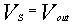 When Vs is greater than battery1, then
diode1 closes the branch and current is allowed to flow down this
branch. Diode2 holds its branch open and no current is allowed
across its branch. By writing a KCL equation at the node above
diode1 as the sum of all currents leaving the node we get for
Vs < 4.5V: When Vs is greater than battery1, then
diode1 closes the branch and current is allowed to flow down this
branch. Diode2 holds its branch open and no current is allowed
across its branch. By writing a KCL equation at the node above
diode1 as the sum of all currents leaving the node we get for
Vs < 4.5V:
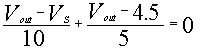
When Vs is greater than battery2,
then diode2 closes the circuit and current is allowed to flow down
this branch. Diode1 holds its branch open and no current is allowed
across its branch. By writing a KCL equation at the node above the
diode as the sum of all currents leaving the node we get for
Vs > 5.5V:
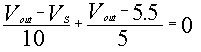 |




