| The voltage across a 200 milli-henry inductor
is given as:
| v(t) |
= (1-3t)e-3t mV |
t > 0 |
|
= 0 |
t < 0 |
Find
and plot the waveforms for current, energy, and power.
Irwin. page 264 example 6.7
The graph of the current was created using the pcewise program.
- From -infinity to: 0
Graph the line:0.
- From 0 to:infinity
Graph the
line:(1-3t)e-3t.
- Set the graph window variables as shown.
To graph the
current, power, and energy, from the voltage we need the
relationships.Given the voltage, the current can be found by:
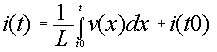 |




