Utilisation de menuz()

• Introduction et écran principal
• F1 Voir
• F2  Remise à zéro
• F3 Calculs d'impédances
• F4 Passage structure série-structure parallèle et l'inverse
• F5 Calculs de modules et arguments 
• F6 Diviseur de courant et de tension
• F7 Solveur
• Télécharger programme pour TI89
• Télécharger programme pour TI92 92+ et Voyage 200
• Télécharger la nouvelle version pour TI92+ et Voyage 200
  
• Télécharger la notice complète des programmes 
• Télécharger les polices TI pour lire le document word 
• Exemple d'utilisation: La première interro de Terminale STI en 8 écrans
  

Attention! la variable "omega" créant des problèmes, je l'ai remplacée par w (double vé)il se peut que quelques omega trainent encore de ci de là!
Je laisse les anciennes versions, car j'ai supprimé quelques ponts d'impédances qui peut-être peuvent servir. A qui? ça j'en sais rien!

Introduction et écran principal
Comme son nom l'indique presque, il sert à faciliter les calculs (numériques ou litteraux) utilisant les nombres complexes sur les impédances. Lancer le programme menuz() puis faire .
Refaire pour revenir au menu d'origine. Les nouveaux menus déroulants sont toujours présents au redémarrage s'ils n'ont pas été enlevés.

Les différentes fonctions:

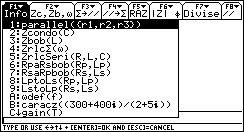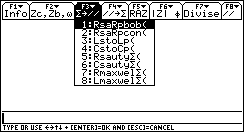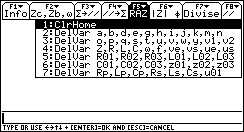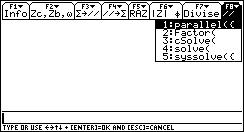
Appuyer sur le bouton stop(Netscape) ou Arrêter(IE4) de votre navigateur pour fixer un écran.

F1 : voir
Observer le résultat de la fonction créée et savoir quelles sont les variables utilisées par cette fonction.

F2 remise à zéro

F3 Calculs d'impédances: 

1. wsifegal(f) renvoi la pulsation w = 2.pi.f;
2. zcondo(C)renvoi l'impédance complexe de c:
3. zbob(L) renvoi l'impédance complexe d'une inductance pure l: i.l.w
4. ZrlcSeri(R,L,C) donne l'impédance complexe de R,L et C en série en fonction de w.
5. ZrlcPara(R,L,C) idem pour RLC parallèle. Pour une forme compacte ajouter Factor( devant (F8-2).
6. zrlcSdew(w) donne le module de RLC série.
7. zrlcPdew(w) idem pour RLC parallèle.
8. parallel({z1,z2,z3}) calcul ou expression de l'impédance équivalente au groupement Z₁, Z₂ et Z₃ en parallèle.
9. Cserie( condensateurs en série
10. A. Factor( voir plus loin

F4 Passage de la structure série à la structure parallèle (//) et inversement

1. Rs2Rpbob(rs,ls,w) passage de R_S à R_P pour une bobine définie par R_S et L_S .
2. Rs2Rpcon(rs,cs,w) passage de R_S à R_P pour un condensateur défini par R_S et C_S.
3. Rp2Rsbob( rp,lp,w) passage de R_P à R_S pour une bobine définie par Rp et Lp .
4. Rp2Rscon(rp,cp,w) passage de Rp à Rs pour un condensateur défini par Rp et Cp
5. Cs2Cp(rs,cs,w) passage de Cs à Cp
6. Cp2Cs(rp,cp,w) passage de Cp à Cs
7. Ls2Lp(rs,ls,w) passage de L_S à L_P pour une bobine définie par R_S et L_S .
8. Lp2Ls(rp,lp,w) passage de Lp à Ls pour une bobine définie par Rp et Lp.

F5  |Z| phi calculs de modules et arguments

1. module(z) donne le module (idem abs(z), mais en français)
2. argument(z) donne l'argument (vérifier le mode radian ou degré)
3. ab2modar(a,b) pour un complexe sous la forme a + jb donne [module; argument]
4. modar2ab(module,argument) pour un complexe sous la forme [module; argument] donne a + jb
5. gain(T) donne 20.log(T). Oui, oui 20.log(t) = 8,68588963806ln(t), j'ai vérifié!
6. zrlcSdew(w) donne le module de RLC série.
7. zrlcPdew(w) idem pour RLC parallèle.

F6 Diviseur de tension et de courant:

1. divtens(utotal,z1,z2): diviseur de tension: donne l'expression de la tension u₁ aux bornes de Z₁. u_total appliquée à Z₁ et Z₂en série.
2. divcour(itotal,z1,z2): diviseur de courant: donne l'expression du courant i₁ dans Z₁.
3. divcourN(itotal,{z1,z2,z3...}): les courants dans Z₁, Z₂... et divcourN(itotal,{z1,z2,z3...})[2] pour le courant dans Z₂.
4. superpos(v1,z1,z2,v2): théorème de superposition: donne la tension u entre Z₁ et Z₂ avec, à gauche(en entrée) v₁ et à droite(en sortie) v₂

F7 Solveur

1. Factor( factorise l'expression d'un nombre complexe qui par défaut est donné sous la forme a + jb
2. csolve( voir doc
3. Solve(: voir exemple montage amplificateur inverseur à aop.
4. syssolve({eq1,eq2...},{var1,var2...})
   Exemple:syssolve({x+2=3y,2y-4x=8},{x,y})
   Résultats: {x=2, y=0}.

F5 Deux nouvelles fonctions ajoutées

• modar2ab() transforme le complexe sous la forme [module;argument] en a+jb et
• ab2modar() transforme le complexe a + jb sous la forme [module;argument]

ATTENTION! si la calculatrice est en mode degré entrer l'argument en degré

[Retour page d'Accueil] [Exemple d'utilisation]

---

©maj 2010 - Loverde Christian, Physique Appliquée
Lycée Jaufré Rudel BLAYE 33390