Blaye le 20 mai 1999
Première STI, Devoir n° 7
PHYSIQUE APPLIQUEE
Dans tout le devoir et chaque fois que cela sera nécessaire il est demandé de faire un schéma du circuit. L'application numérique ne pourra que suivre l'application littérale.
Problème 1:CIRCUIT RC EN RÉGIME SINUSOÏDALE + L
Aux bornes d'un circuit comprenant en série une résistance non inductive R = 300 W, un condensateur de capacité C = 8 µF, on applique une tension qui prend les valeurs:
u(t) = [8,484 sin(314t + f)] V
1. Indiquer la tension efficace aux bornes du circuit ainsi que la fréquence du courant.
2. Calculer l'intensité du courant dans ce circuit ainsi que les valeurs efficaces U1 de la tension u1(t) aux bornes de la résistance et U2 de la tension u2(t) aux bornes du condensateur.
Vérifier ces valeurs avec la construction de Fresnel ( échelle: 2 cm pour 1 V).
Calculer le déphasage f de la tension u(t) par rapport à i(t) en radian SVP.
3. On relie les bornes de la résistance à un oscilloscope dont la sensibilité verticale est réglée sur 2V/div, quelle est l'amplitude de la courbe obtenue après mise en route du balayage horizontal?
On utilise maintenant l'oscilloscope en bicourbe. Il permet de visualiser, en concordance de temps les tensions u1(t) et u(t). Sachant que la vitesse de balayage est réglée sur 4ms/div, calculer le décalage q observé à l'écran entre les deux courbes en ms puis en divisions.
4. Déterminer la valeur de l'inductance pure L qu'il faut placer en série avec le circuit précédent pour l'impédance soit de 400 W.
Quelle inégalité doit vérifier la valeur de L pour que la tension u(t) soit en retard sur i(t)? Justifier la réponse (it's quite easy!).
Problème 2:CIRCUIT RL EN RÉGIME SINUSOÏDALE
On dispose d'une bobine dont on veut, en régime sinusoïdale, mesurer l'inductance L et la résistance X, et de trois voltmètres permettant de mesurer des tension efficaces.
Pour cela on réalise le montage suivant: la bobine étudiée est placée en série avec une résistance R = 5 W non inductive. Aux bornes de l'ensemble on établit une tension sinusoïdale de fréquence 50 Hz.
Le voltmètre placé aux bornes de la bobine indique U1 = 6,63 V, celui placé aux bornes de la résistance indique U2 = 1 V; enfin le troisième placé aux bornes de l'ensemble, indique U = 7V.
1. L'intensité instantanée dans le circuit étant i(t) = I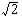
sin wt, donner les expressions des tensions instantanées u1(t), u2(t), u3(t) respectivement aux bornes de la bobine, de la résistance R et de l'ensemble. Faire la construction de Fresnel.
2. Calculer :
w l'intensité efficace I du courant,
w l'impédance Z de l'ensemble,
w l'impédance Z1 de la bobine.
3. Déduire des résultats précédents les valeurs de L et de X.
Problème 3:AMPLIFICATEUR DE MOYENNE PUISSANCE
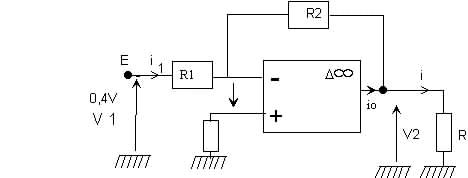
R1 = 2,2 kW, R2 = 22 kW, R = 100 W.
1. Exprimer v1 en fonction de e , i1 , R1 et exprimer v2 en fonction de e , i1 , R2 .
Calculer AV0 =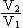
en fonction de R1 , R2 .
2. Calculer la tension v2 et i le courant traversant R.
3. Calculer l'intensité du courant i0 en sortie de l'amplificateur opérationnel.
4. Quelle valeur de v1 sature l'Aop? Quelle est la valeur de i correspondante?
Problème 4:TRANSFORMATION DE THÉVENIN
Dans le montage ci-dessous on donne: R = 4 kW; I = 9 mA; E1 = 12 V; E2 = 24 V
1. Déterminer le générateur Thévenin équivalent au dipôle AB.
2. Calculer l'intensité du courant traversant une résistance RAB = 2 kW.
[Autres devoirs]