Blaye le 5 février 1999
Première STI, Devoir n° 5
PHYSIQUE APPLIQUEE
Dans tous les exercices proposés ci-dessous, les Amplificateurs Intégrés Linéaires sont supposés idéaux. La tension de saturation vaut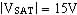 
I. Montages à Amplificateurs Intégrés Linéaire:
Montage 1:
On donne: R1 = 4,7 kW; R2 = 47 kW; RC = 1 kW; Ve tension continue de valeur: Ve = 0,2 V.
1. Quel est le mode de fonctionnement de l'A.I.L.?
2. Déterminer la relation entre Ve et VS. En déduire l'amplification en tension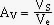 
du montage.
3. Quelle est la valeur maximale de Ve qui permet au montage de fonctionner encore en mode linéaire?
Calculer, dans ce cas, la puissance maximale fournie à la charge RC.
Montage 2:
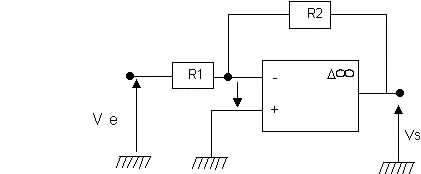
On donne: R1 = 4,7 kW; R2 = 47 kW; ve(t) tension triangulaire de valeurs etrèmes: Vemax = 0,2 V et Vemin= -0,2V
1. Déterminer la relation entre Vemax et VSmax. En déduire l'amplification en tension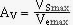 
du montage.
2. Représenter sur un même système d'axes, avec des échelles appropriées les tensions ve(t) et vS(t). II. Électromagnétisme:
Force électromagnétique:
Le conducteur dans sa position PQ et dans sa position P'Q' ainsi que l'aimant en U sont horizontaux.
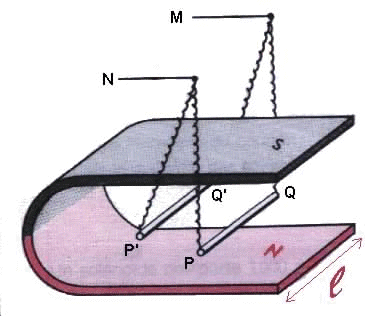
1. Préciser la direction et le sens du champ magnétique à l'intérieur de l'aimant en U.
2. Le conducteur PQ, parcouru par un courant I, est soumis à une force électromagnétique. Il est déplacé vers la position P'Q'. En déduire la direction et le sens de la force électromagnétique, de point d'application: milieu de PQ, qui s'exerce sur le conducteur. En déduire le sens du courant traversant le conducteur.
3. A.N.: B = 0,735 T; I = 2,5 A; PQ = 5 cm; l = 4 cm. Calculer l'intensité de la force électromagnétique.
Champ magnétique résultant:
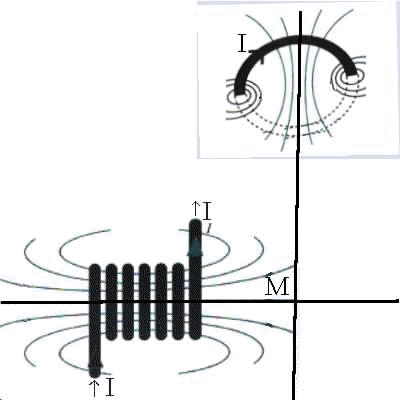
Les axes des deux bobines sont perpendiculaire.
1. Refaire dans un plan le schéma du dispositif et représenter les champs magnétiques créés par les deux bobines au point M. Par une construction graphique, représenter le champ résultant en M. Le champ magnétique terrestre est négligeable devant les champs créés par les deux bobines.
2. Application numérique: µ0 = 4p10-7 USI
2.1. Bobine longue: N = 70 spires; I = 10 A; L = 12 cm. Caculer le champ BC1 au centre de la bobine longue. Le champ BM1 en M est 10% du champ au centre de la bobine longue.
2.2. Bobine plate: N' = 400 spires; I = 1 A; R = 50 cm. Caculer le champ BC2 au centre de la bobine. Le champ BM2 en M est 80% du champ au centre de la bobine plate.
2.3. Calculer BM, le champ résultant en M
III. Transformation de Thévenin-Norton:
Modèle équivalent Thévenin d'un circuit:
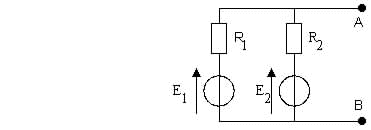
1. Déterminer les éléments du modèle équivalent de Thévenin du circuit ci-dessus.
2. En déduire la tension aux bornes d'une résistance R3 placée entre A et B.
3. Application Numérique: R1 = 10 W; R2 = 20 W; R3 = 60 V; E1 = 12 V; E2 = 4 V.
Modèle équivalent Norton d'un circuit:
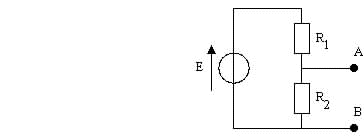
1. Déterminer les éléments du modèle équivalent de Norton du circuit AB ci-dessus.
2. En déduire l'intensité du courant traversant une résistance R3 placée entre A et B.
3. Application Numérique: R1 = 10 W; R2 = 20 W; R3 = 60 V; E = 12 V.
IV. Les condensateurs:
Charge d'un condensateur à courant constant:
1. On donne I = 50 µA. Calculer les coefficients directeurs des deux droites. En déduire la capacité de chaque condensateur.
2. Calculer la capacité de l'association parallèle des deux condensateurs. En déduire le coefficient directeur de la droite obtenue en chargeant cette association avec le même courant.
[Autres devoirs]