Nombres complexes et fonctions sinusoïdales
A une fonction sinusoïdale on fait correspondre un nombre complexe:
La tension u(t) = U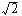
cos(w.t+f) sera représentée par le nombre complexe U = [ U; f].
v U nombre complexe représentant u(t)
v U module de U = U valeur efficace de u(t)
v f argument de U = phase de u(t) à l'origine des temps.
Les nombres complexes:
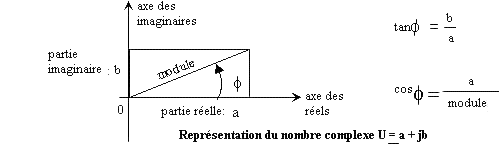
Tension complexe: U = a +j.b v module U =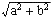 
v Argument f: tanf =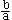 
ATTENTION!! La fonction Arctangente (tan-1 dans les calculatrices) donne un angle compris entre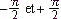 
. Si a = -3 et b = 2 le résultat donné est le même que pour a = 3 et b = -2 pourtant:
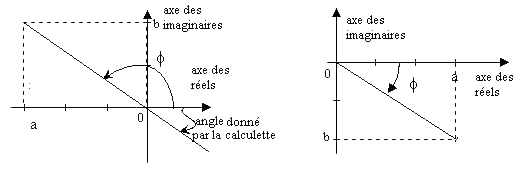
Quand la partie réelle est négative l'angle n'est pas compris entre 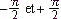il faut ajouter p au résultat ou 180° si on travail en degré.
Avec a = -3 et b = 2 la calculette donne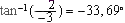 
f = -33,69+180 = 146,31°
a = 3 et b = -2 la calculette donne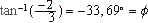 
On peu aussi utiliser la fonction renvoyant les coordonnées polaires (module et argument) à partir des coordonnées cartésiennes x (partie réelle a) et y (partie imaginaire b):
CASIO: Pol(a,b) renvoie l'argument dans J et le module dans I.
TI 80 et TI 82: R >Pr(a,b) donne le module et (menu angle 3)
R >Pq(a,b) donne l'argument (menu angle 4)
TI 81: R >P(a,b) renvoie le module et l'argument est dans q.
TI 85: menu CPLX abs(a,b) donne le module
angle(a,b) donne l'argument.
TI 92 ou TI 89: abs(a + i.b) donne le module
angle( a + i.b) donne l'argument.
TI92 ou 89 et menuz() module(a + i.b) donne le module
argument( a + i.b) donne l'argument.
[Autres devoirs]