Classe de Terminale STI
BORDEAUX 1995
Epreuve: PHYSIQUE APPLIQUEE
(Durée: 4h - Coefficient: 5)
Le schéma, qui est donné figure 6, est celui d'un interrupteur unidirectionnel commandé. Pour que celui-ci conduise, il faute que le potentiel d'anode A soit supérieur à celui de la cathode C et qu'une tension Vcc soit appliquée entre l'entrée de commande ou gachette G et la cathode, sous forme d'un train d'impulsions positives.
L'étude porte sur l'obtention de ce train d'impulsions et sa synchronisation sur un autre signal.
Tous les amplificateurs intégrés seront considérés comme parfaits (courants d'entrée négligeables, résistance de sortie nulle). Ils sont alimentés sous des tensions symétriques +Vcc et -Vcc avec Vcc = 15 V. On suppose de plus que leurs tensions de saturation sont égales à +Vcc et -Vcc.
Les diodes sont considérées comme parfaites : leur tension directe est nulle quand elles conduisent.
Le circuit intégré 555 de la figure 4 est alimenté sous la tension Vcc = 15V.
La commande de l'interrupteur est synichronisée sur une tension v1(t) sinusoïdale, de fréquence 50 Hz.
A - Etude du circuit déphaseur
Le circuit est représenté sur la figure 1(R1 = 10 kW):
L'amplificateur opérationnel fonctionne en régime linéaire. V1 , V2, sont les nombres complexes associés respectivement aux tensions sinusoïdales v1(t) et v2(t). U+ et U- sont les nombres complexes associés respectivement à u+ potentiel de l'entrée non inverseuse et u- potentiel de l'entrée inverseuse de l'amplificateur opérationnel.
1. Exprimer U+ en fonction de V1 , R1 , C1 et w.
2. Exprimer U- en fonction de V1 , V2 .
3. En déduire l'expression de l'amplificati.on,en tension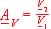 
Montrer que AV s'exprime par:
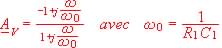
4. Montrer que le module AV de AV est tel que AV = 1.
5. On donne R1 = 47 kW, quelle valeur faut-il donner à C1 pour que, à la fréquence f = 50 Hz, de la tension de synchronisation v1(t) , le rapport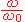 
soit égal à 1 ?
6. Détermination de j, déphasage entre v2(t) et v1(t).
On se place dans le cas où la condition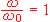 
est réalisée.
6.1. Méthode expérimentale:
Le graphe de la feuille réponse page 8 donne les relevés, en concordance de temps, à l'oscilloscope des tensions v1(t) et v2(t); on a v1(t) = V1max sinwt avec V1max = 13 V.
6.1.1. Déterminer graphiquement le déphasage j entre v2(t) et v1(t). On précisera celle de ces deux tensions qui est en avance par rapport à l'autre.
6.1.2. Quelle est l'aimplitude de v2(t) ? Ce résultat est-il cohérent avec l'étude dans les questions précédentes.
6.2. Méthode théorique :
6.2.1 Donner l'expression de AV lorsque la condition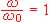 
est réalisée.
6.2.2 Montrer que AV = j. En déduire la phase de v2(t) si l'origine des phases est déterminée
par v1(t). Comparer avec le résultat de la mesure.
B - Fonction comparateur ( figure 2 )
(R2 = R3 = R4 = 10 kW D1 parfaite)
Ucom est une tension continue constante, réglable, telle que 0 < Ucom < 13V.
1. Quel est le mode de fonctionnement de l'amplificateur A02 ?
2. Pour Ucom < v2(t) quelle est la valeur de la tension v3(t) ?Quel est l'état de la diode D1 , en déduire la valeur que prend v4(t).
3. Répondre aux même questions pour Ucom > v2(t).
4. Application
Représenter v4(t) sur le graphe de la feuille réponse page 8 à joindre à la copie, en concordance des temps avec v2(t), pour Ucom = 7,0 V.
5. On note t1 l'instant positif où, pour la première fois, v2(t ) devient inférieure à Ucom et t2 l'instant où pour la première fois après t1, v2(t ) devient supérieure à Ucom ; on écrit v2(t) = V2maxcoswt.
On pose a = wt1 ; w sera l'angle de retard à l'ouverture de l'interrupteur commandé.
Donner une relation entre cosa , Ucom et V2max.
6. Avec Ucom = 7,0 V; V2max = 13 V et f = 50 Hz, calculer a (en radians) puis t1 .
C- Circuit impulsionnel ( figurer 3 )
La diode D2 est considérée comme parfaite.
Entre l'instant t = 0 et, l'instant t1 (instant où v4(t) bascule à 0V) le condensateur de capacité C2 n'est pas chargé.
1. Pour t = t1- préciser la valeur de la tensicin v4(t1-), et celle de la tension v5 (t1-).
2. A t = t1+ quelle est la valeur que prend v4 ? Que devient alors la valeur de v5(t1+) ?
3. Tracer le circuit équivalent de charge du condensateur. La diode D2 intervient-elle dans cette phase ? Que peut-on dire de v5(t) par rapport à vC2 ?
4. On donne R5 = 10 kW, C2 = 10 nF.
Calculer la constante de temps de ce circuit de charge du condensateur.
Au bout de combien de temps peut-on estimer le condensateur presque totalement chargé? Quelle est alors la tension atteinte par v5(t) ?
Soit t2 l'instant où v2 devient supérieure à Ucom.
5. A t = t2- que valent les tensions v4(t2-), v5(t2-) et vC2(t2-)?
6. A t = t2 , v4(t) bascule de 0 V à Vcc. Quelle serait, s'il n'y avait pas la diode D2, la tension v5(t2+)?
7. Quel est alors l'état de la diode D2 , quel rôle joue-t-elle? Quelle est la valeur de la tension v5(t) à partir de l'instant t2+ ?
8. Dessiner l'allure de la tension v5(t) en concordance de phase avec v4(t) sur la feuille graphique page 8 à joindre à la copie.
D-Etude du monostable utilisant le circuit 555 ( figure 4 )
Le potentiel du point A est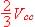 
, celui du point B est 
.
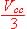Quand le transistor T' est saturé, on néglige sa tension collecteur-émetteur de saturation.
La tension de commande v5(t) est représentée sur le graphe de la feuille-réponse page 8.
1. Dans l'intervalle de temps [O , t1 ] la tension v6, est nulle et le transistor T' est saturé; dans cet intervalle la tension v5(t) vaut +Vcc .
1.1. Quels sont les valeurs des tensions v' et vC3 ?
1.2. Quels sont les états logiques des sorties R et S des comparateurs A03 et A04 ?
2. Etude de l'évolution des grandeurs à partir lu temps t = t1
A t = t1 la tension v5 bascule de Vcc à 0.
2.1. Quelle est la valeur logique de S ? QueIle est celle de la sortie Q ? Quel est l'état de T' ? Que vaut v6 ?
2.2. Quelle est l'expression de la constante de temps t avec laquelle évolue vC3 ?
2.3. A l'instant t = t3 vC3 prend la valeur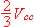 
; pour t > t3 , quel est l'état de T' ? Quelle est la
valeur de v6 ?
3. On définit q = t3 - t1.
Il est rappelé qu'un condensateur dont la tension v évolue exponentiellement avec la constante de temps t vers une limite asymptotique V¥ (pour t tend vers ¥ ) met, pour passer d'une tension Vi à une tension Vt, une durée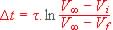 
3.1. Exprimer q en fonction de R6 et C3.
3.2. Calculer q avec R6 = 100 kW et C3 = 10 nF.
4. Tracer, en concordance de temps avec v5(t), le graphe de v6(t) sur la feuille réponse n°8.
E-Elaboration du train d'impulsions ( figure 6 )
La porte logique reçoit sur une entrée le signal v6(t) et sur l'autre un signal d'horloge à la fréquence 10 kHz. Donner l'allure du signal de sortie v7(t) de cette porte en cncordance de phase avec v6(t), sur la feuille réponse page 8 ,à joindre à la copie.
