Classe de Terminale STI
Baccalauréat Sti 1988
On se propose d'étudier un système réalisant la conversion d'une vitesse de rotation d'un moteur, en une tension.
Le système est représenté par le schéma synoptique suivant (fig. 1):
La lecture de la tension v6 se faisant au voltmètre continu, le dispositif doit réaliser la conversion vitesse - tension telle que v6 = k.n avec v6 en volts et n en tour.s-1.
Le capteur permettant de transformer la grandeur physique ( la vitesse de rotation du moteur ), en tension électrique, ne sera pas étudié ici. Il suffit de savoir qu'il délivre une tension sinusoïdale d'amplitude fixe, mais dont seule la fréquence varie avec la fréquence de rotation du moteur.
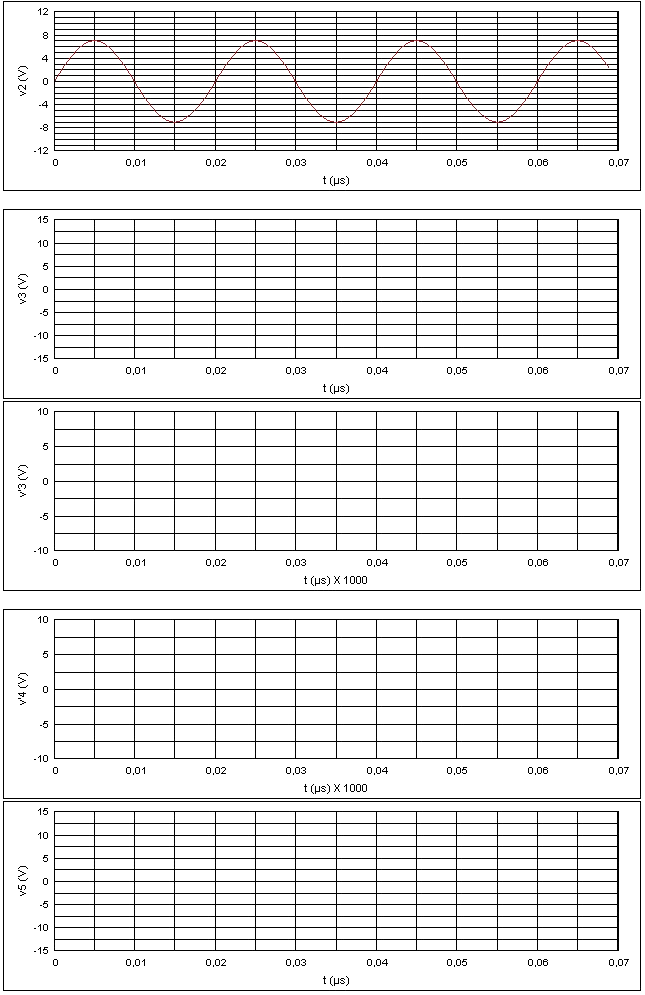
v1(t) tension sinusoïdale de valeur max V1max
{ Chaque fonction pourra être traitée de façon indépendante;
{ Tous les circuits intégrés linéaires sont compensés, considérés comme parfaits et alimentés en ± VCC = ± 15 V.
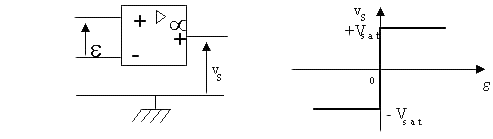
{ La tension de saturation est :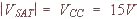 
Pour les applications numériques, on utilisera également les valeurs indiquées sur les figures.
I. ÉTUDE DE L'AMPLIFICATEUR: (fig. 2)
La tension v1 fournie par le capteur a une amplitude V1m de 200 mV. On désire traiter un signal plus important, dont on se fixera l'amplitude à V2m = 7V.
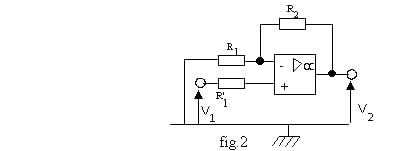
1.1. Exprimer AV, amplification en tension du montage, en fonction de R1 et R2.
1.2. Calculer la résistance R2 que l'on devra choisir si la résistance R1 vaut 20 kW.
1.3. Quel est le rôle de la résistance R'1? Donner une valeur approchée de la résistance que vous prendrez.
II. ÉTUDE DU CIRCUIT DE MISE EN FORME: (fig.3).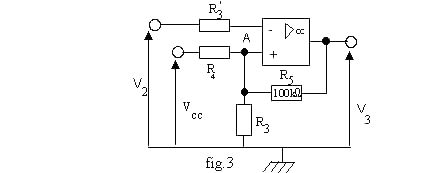 
2.1. Donner le schéma équivalent de Thévenin de l'ensemble R3 , R4 , VCC , vu entre le point A et la masse M, et exprimer les éléments R0 et U0 du circuit équivalent en fonction de R3 , R4 et VCC .
2.2. Donner un schéma simplifié du montage.
2.3. A partir des 2 valeurs que peut prendre v 3 , exprimer v A sous la forme suivante :
v A = Vm ± DV
2.4. Expliquer le fonctionnement du montage. Représenter v 3 = f(v 2) en faisant apparaître les seuils de basculement supérieur et inférieur: VH et VB.
2.5. On désire obtenir les valeur numériques suivantes: VH = 5 V et VB = -1 V. A partir de l'expression de DV, vérifier que la valeur de R0 est de 25 kW. A partir de l'expression de Vm vérifier que la valeur de U0 est de 2,5 V.
2.6. Déterminer alors les valeurs numériques des résistances R3 et R4 du montage de la fig. 3.
2.7. Représenter v 3(t) sur la feuille réponse.
III. ÉTUDE DU DÉRIVATEUR: (fig. 4).
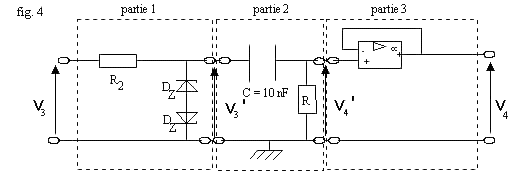
Diode Zener DZ : UZ = 4,3 V; Ud = 0,7 V.
On rappel qu'un front montant d'amplitude E, appliqué à un
circuit R-C, à l'instant t = 0, crée un courant transitoire dont
l'expression mathématique est i(t) =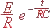 
.
3.1. Analyser le fonctionnement de la partie 1 (la tension v 3 est une tension rectangulaire alternative d'amplitude 15 V). Représenter, sur la feuille réponse, la tension v'3 (t).
3.2. Analyser le fonctionnement de la partie 2 lorsque la tension v 3 est appliquée à l'entrée de la partie 1. Préciser au bout de combien de temps la tension v'4 pourra être considérée comme nulle.
3.3. Représenter, sur la feuille réponse, la tension uC(t). Exprimer v'4 en fonction de v'3 et uC.
Représenter la tension v'4 (t). Quelle est la fonction de cette partie 2 du montage?
3.4. Préciser la fonction réalisée par la partie 3 du montage et justifier son rôle.
IV ÉTUDE DU MONOSTABLE À CIRCUIT INTÉGRÉ LINÉAIRE: (fig. 5)
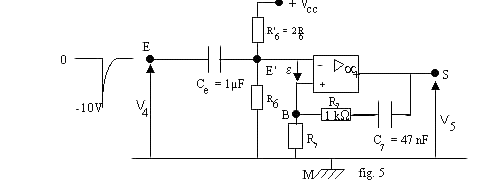
Pour trouver l'état de repos du monostable, on supposera que cet état existe depuis un certain temps. Les régimes transitoires ont disparu, aucun courant ne traverse les condensateurs.
4.1. Trouver l'état de repos de ce monostable ( v 4 = 0, pas de courant dans C7 et R7 ) en précisant les tensions v E'M ; v BM et v 5.
4.2. A l'instant t = 0, on applique en E une impulsion négative d'amplitude 10 V. Donner à t = 0, les tensions v E'M ; v BM ; e ; v 5 .
4.3. Donner, à l'instant t = 0+, juste après l'impulsion, la tension v BM. Quel est le sens du courant qui apparaît à partir de ce moment là dans la branche SBM?
Montrer que l'évolution de v BM(t) peut s'écrire sous la forme:
v BM(t) = VCC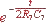 
.
4.4. Pour quelle valeur de v BM la tension de sortie v 5 bascule-t-elle à nouveau?
Montrer que la durée du monostable à pour expression q = 2R7C7Ln3.
4.5. Que se passe-t-il si, au lieu de l'impulsion négative envisagée au 4.2., on applique en E, une impulsion positive de +10 V?
4.6. Représenter la tension v 5 sur le document réponse.
V ÉTUDE DU REDRESSEUR ET DU FILTRE: (fig. 6).
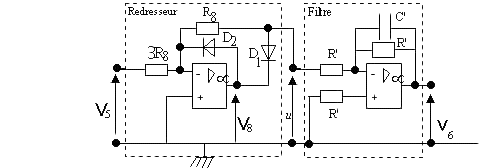
5.1. Etude du redresseur: R8 = 12 kW; les diodes sont supposées idéales.
{Pour chaque alternance de la tension v 5 , préciser l'état des diodes D1 et D2.
{ Vérifier le fonctionnement linéaire du montage dans chaque cas, en déduire alors la valeur de u.
{ Donner l'allure de u(t) si la tension v 5 est une tension rectangulaire, alternative d'amplitude 15 V.
5.2. Etude du filtre: C' = 1 µF; R' = 330 kW.
Pour cette étude, et pour et pour cette étude seulement, on supposera que la tension u(t) est sinusoïdale de fréquence f .
{ Calculer l'amplification A'V =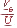 
.
{ Calculer le gain GV = 20 log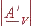 
pour une fréquence f = 0 Hz et pour une fréquence f = 500 Hz.
{ Pour quelle fréquence aura-t-on un gain de - 20 dB?
{ La tension u étant périodique et unidirectionnelle, qu'indiquera la valeur de la tension v 6?
VI ÉTUDE DU SYSTÈME TOTAL:
6.1. v 6(t) est une tension unidirectionnelle de période T, dont les variations en fonction du temps sont les suivantes:
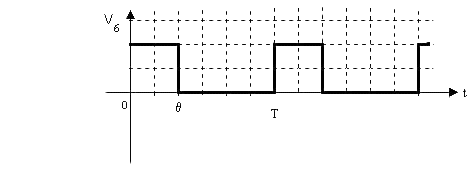
Evaluer sa valeur moyenne que l'on notera V6moy .
6.2. Montrer que la tension mesurée est bien de la forme V6moy = k.n. Exprimer k en fonction des caractéristiques du montage.
6.3. Quelle est la fréquence maximum qu'un tel montage permet de mesurer?
