Coef 5 Durée : 4 heures
Série: S.T.I. GÉNIE ÉLECTRONIQUE
Épreuve: PHYSIQUE APPLIQUÉE
le LM 13700
- Ce circuit permet la réalisation de nombreuses fonctions de l'électronique analogique linéaire et
non linéaire.
On se propose de réaliser à l'aide de ce circuit intégré
- un filtre passe bas dont la fréquence de coupure est contrôlable par un courant.
- un oscillateur sinusoïdal modulable en fréquence par un courant.
Ces trois études sont indépendantes et se réfèrent à l'introduction suivante:
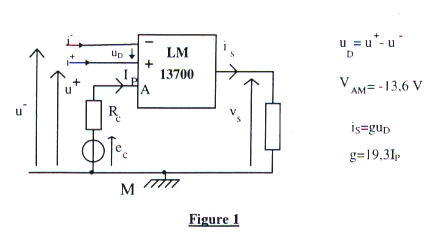
Introduction: Le circuit sera représenté comme sur la figure 1, page7.
Propriétés :
- En boucle ouverte et en réaction négative le circuit peut,fonctionner en régime linéaire. Pour ce régime
iS = g uD avec g = 19,3 Ip Ip > 0 , g en siemens et Ip en ampères.
(1) (2)
Ces expressions sont valables en statique et en régime sinusoïdal jusqu'à des fréquences de l'ordre de 100 kHz.
Pour une alimentation symétrique 
15 V du circuit LM 13700, la ddp VAM est constante et vaut - 13,6 V.
VAM = -13,6 V valable pour tout le problème.
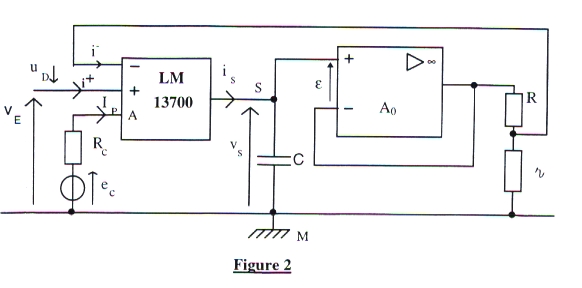
I Réalisation d'un filtre dont la fréquence de coupure est contrôlable par un courant.
Voir figure 2
Hypothèses
v Pour le circuit LM 13700, les courants d'entrée i+ et i- sont nuls.
v VE, uD, iS, vS sont des fonctions sinusoïdales du temps de pulsation w. VF, UD, IS, sont les nombres complexes qui leur sont associés.
v L'amplificateur A0 est un amplificateur opérationnel fonctionnant en régime linéaire. On le
supposera idéal (ce qui implique notamment l'égalité e = 0).
Questions :
1. Exprimez IS en fonction de VS, C, w).
2. Exprimez UD en fonction de VE, VS, r, R.
3 En vous aidant de l'expression (1) donnée en introduction et des deux résultats précédents, donnez la relation liant VS et VE.
4 On considère la transmittance complexe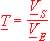 
. Elle peut s'écrire:
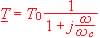
4-1 Donnez les expressions de T0 et de wc. Calculez To si r = 220 W et R = 100 kW.
4-2 Quelle est la valeur limite de T lorsque la pulsation w tend vers zéro ?
5 Exprimez Ip en fonction de ec, RC, VAM .
r = 220 W R = 100 kW RC = 33 kW C = 270 pF
Compte tenu des données de l'introduction, montrez que la fréquence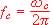 
peut s'écrire sous la forme
fc = a ec + b
Donnez les valeurs de a et de b ; sachant que ec varie de -5 V à +5 V, montrez que les valeurs
extrêmes de fc sont voisines de 6,5 kHz et 14 kHz.
6 Pour ec = -5,0 V, C = 2,7 nF on prend fc = 650 Hz
Si la condition "f très supérieure à fc " est réalisée, on peut écrire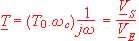 
Il en résulte que j wVS = (T0 wc)VE .
On rappelle que si Vs est associé à vS(t), alors j w VS est associé à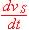 
.
6.1 Lorsque la condition précédente est réalisée, quelle est la fonction réalisée par le montage de la figure 2?
6.2 On applique à l'entrée du filtre un signal carré périodique, de valeur moyenne nulle, de fréquence fE = 6,5 kHz.
Sachant que les harmoniques de rang pair ont une amplitude nulle pour ce signal, quelles sont les fréquences des 5 premières composantes sinusoïdales non nulles de vE(t) ?
La condition "f très supérieure à fc" est-elle réalisée pour chaque harmonique ? Quelle est alors la forme d'onde de vS(t) ?
7 C est désormais la somme : de la capacité Cc d'un condensateur placé entre S et M et d'une capacité parasite CP éventuelle: C = CC + CP
CC = 270 pF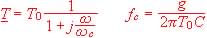 
( r, R et Rc inchangées)
7.1 On visualise vS(t) sur l'écran de l'oscilloscope.
7.1.1 On n'utilise pas de sonde compensée en fréquence. On considère que l'impédance d'entrée de l'ensemble {cablecoaxial,oscilloscope } est purement capacitive de valeur 130 pF: CP = 130 pF.
Lors d'une excursion en fréquence, quelle fréquence de coupure mesure-t-on pour le filtre si eC = 0 et si l'oscilloscope est branché entre S et M ?
7.1.2.
On utilise une sonde compensée en fréquenc et l'impédance d'entrée de
l'ensemble {sonde, oscilloscope} est purement résistive de résistance
très grande par rapport à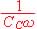 
.
Pour eC = 0, lors d'une excursion en fréquence, quelle fréquence de coupure mesure-t-on?
7.2.
7.2.1. Donnez l'expression du rapport des valeurs efficaces de vS(t) et de vE(t) en fonction de T0 , w, wc.
7.2.2. Exprimez tan q en fonction de w et de wc si q = phase vS(t) - phase vE(t).
7.2.3. Calculez la valeur de |T| pour w = wc.
7.2.4. Pour cette question on utilisera le théorème de superposition:
On applique à l'entrée du filtre une ddp vE qui, exprimée en volts, s'écrit
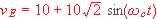
En sortie du filtre on place un voltmètre entre S et M:
v qu'indiquerait un voltmètre RMS (AC + DC) ?
v qu'indiquerait un voltmètre RMS (AC) ?
II Réalisation d'un oscillateur sinusoïdal modulable en fréquence par IP.
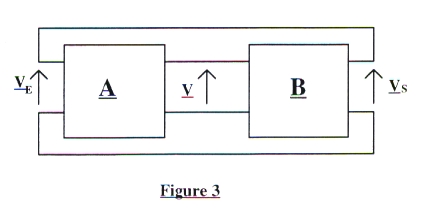
1 L'oscillateur a la structure indiquée sur la figure 3.
On suppose que l'oscillation existe, est sinusoïdale de fréquence f0, de pulsation w0 = 2.p.f0.
1.1. Quelle relation existe-t-il entre A(w0 ) et B(w0 ) ?
1.2. Donnez la relation liant | A(w0 )| et | B(w0)| .
1.3. Donnez la relation la plus générale liant Arg A(w0 ) et Arg B(w0 )
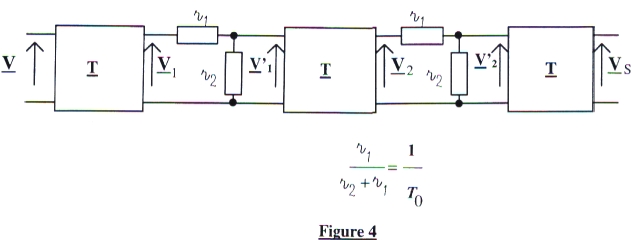
2. Réalisation du bloc de transmittance B : (voir figure 4, page 8).
Il est construit à l'aide de trois filtres du premier ordre de transmittanc complexe:
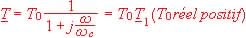
2.1 Donnez l'expression de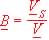 
en fonction de T0 et de Tl sachant que:
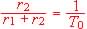
2.2. On pose q1 = Arg Tl et |T1| .
Exprimez Arg B en fonction de q1 et |B| en fonction de T0 et de Tl.
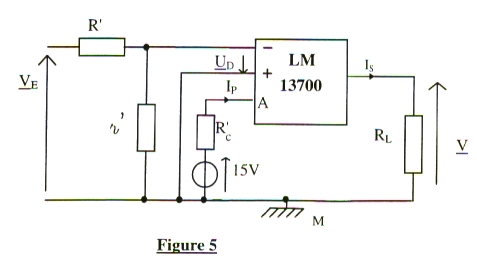
3. Réalisation du bloc de ~transmittance A (voir ~fi-ure 5).
3.1. Donnez l'expression de UD en fonction de VE, r', R'.
3.2. Exprimez V en fonction de IS et de RL .
3.3. En déduire l'expression de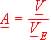 
. compte tenu du (1) de l'introduction.
Par la suite on posera Arg A = p et A = |A|.
4. Expression de la fréquence d'oscillation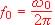 
On suppose le système bouclé et oscillant sinusoïdalement à la fréquence f0:
4.1. En utilisant les relations des questions 1.2, 1.3, 2.1 et 3.3, établir une relation entre A, T0, T1.
Calculez la valeur de q1 sachant que celle-ci est comprise entre 0 et -p/2.
4.2. Sachant que tan q1 = -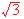
, en déduire la valeur du rapport 
.
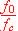4.3. Calculez T1. Calculez A si T0 = 455.
4.4. Sachant que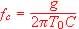 
montrez que f0 est une fonction affine de eC.
Calculez les limites de f0 lorsque eC varie entre -10 V et +10 V:
C = 270 pF T0 = 455 RC = 33 kW
