Classe de Terminale STI
Baccalauréat Sti 1993
Épreuve: PHYSIQUE APPLIQUÉE
Durée 4h; coefficient 5
Remarques générales:
Le sujet comporte trois parties (A, B et C) qui peuvent être traitées de façon totalement indépendante : les résultats nécessaires sont donnés dans le texte.
Lors de la correction, il sera tenu compte de la rédaction et de la justification des réponses sur le fonctionnement des différentes parties du montage.
Les feuilles graphiques 1, 2 et 3 sont à rendre avec la copie.
(conversion niveau de liquide-tension)
Pour réguler la hauteur du niveau d'un bain d'acétone dans une cuve, on utilise un capteur et son conditionneur dans la chaîne de retour de l'asservissement utilisé. Le capteur et le conditionneur doivent transformer une variation de la hauteur du niveau en un signal électrique.
On étudie le fonctionnement du conditionneur qui comporte:
{ un oscillateur à fréquence fixe: partie A,
{ un montage convertisseur capacité - durée: partie B,
{ un filtre: partie C.
Remarque:
Les circuit intégrés sont considérés comme parfaits: intensité d'entrée nulle et résistance de sortie nulle.
A - ÉTUDE DE L'OSCILLATEUR:
L'oscillateur utilisé est un montage astable composé d'un comparateur intégré T1 à deux seuils, rebouclé par un circuit R-C:
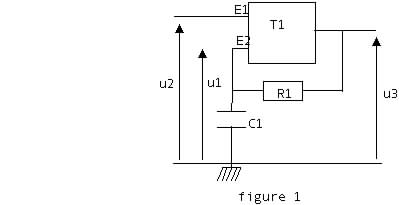
A-1 Étude du comparateur:
Le comparateur T1 est un opérateur logique alimenté sous la tension U0 = 10 V par rapport à la masse.
Ses conditions de fonctionnement sont les suivantes:
ƒ si e2 = 0 alors s = U0 quelle soit la valeur de e1.
ƒ si e2 = U0 alors la sortie dépend de l'entrée e1 :
On donne VP = 6,2 V et VN = 4,1 V.
On veut vérifier ces propriétés. Pour cela, on applique, grâce à un GBF, une tension e1 triangulaire, de valeur moyenne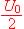 
de valeur crête à crête U0 et de période 300 ms. L'appareil de contrôle est un oscilloscope utilisé en mode XY: e1 est appliquée sur la voie X et s sur la voie Y.
a. Sur la feuille graphique 1 représenter:
ƒLes chronogrammes e1(t) et s(t) en concordance de temps avec e1(t) , lorsque e2 = 0 et lorsque e2 = U0.
ƒL'écran de l'oscilloscope dans les deux cas en y ajoutant le sens de parcours. Dimension de l'écran: 10 cm x 8 cm.
b. Donner les réglages de l'oscilloscope permettant la vérification du fonctionnement du comparateur ( sensibilités des voies, mode de couplage des voies).
Comment peut-on repérer sur l'écran le sens de parcours de la caractéristique?
A-2 Détermination de la période de l'oscillateur en régime permanent:
On impose u2 = U0 = 10 V.
a. A un instant t = 0 pris pour origine des temps, u1 = VN et u3 bascule de 0 V à U0.
Entre l'instant t = 0 et l'instant t1 où u1 est égale à VP , la tension u1 est donnée par l'expression:
u1(t) = U0 + ( VN - U0 ) e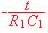
ƒ Dessiner en concordance de temps les allures correspondantes de u1(t) et de u3(t) sur la feuille graphique 2.
ƒ Établir l'expression littérale de la durée t1 .
b. Déterminer les valeurs de u1 et u3 à l'instant t+, juste après l'instant t1.
Entre l'instant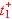 
et l'instant t2 où u1 est de nouveau égale à VN , la tension u1 est donnée en fonction de t par:
u1(t) = VP e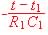
ƒ Dessiner les allures correspondantes de u1(t) et de u3(t) sur la feuille graphique 2.
Pour la suite du problème on donne l'expression littérale de la durée (t2- t1):
t2- t1 = R1C1 Ln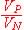
c. Les composants passifs ont les valeurs suivantes: R1 = 4,70 kW ; C1 = 75 nF.
ƒ Calculer numériquement la période T de l'oscillateur astable.
ƒ Calculer le rapport cyclique d de al tension u3. On rappel que le rapport cyclique est égal au quotient de la durée correspondant à l'état haut par la valeur de la période.
Par la suite on admettra que d = 0,50.
B- ÉTUDE DU CONVERTISSEUR CAPACITÉ - DURÉE:
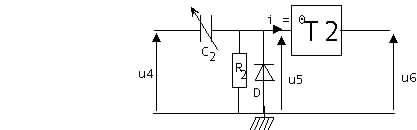
La résistance R2 vaut 120 kW. Le condensateur de capacité C2 est un capteur capacitif plus ou moins plongé dans l'acétone sur une hauteur h et dont la capacité varie avec la hauteur du diélectrique.
B-1 Le montage est placé en cascade à la sortie de l'oscillateur précédent, c'est à dire que l'on établit une liaison directe pour avoir u3 = u4. Pourquoi cette liaison ne modifie-t-elle pas le fonctionnement de l'oscillateur?
Pour que la conversion soit réalisée, il est indispensable que u5 retrouve la valeurs 0 V avant chaque front montant de u4.
B-2 Étude préliminaire sans la diode D:
Pour cette étude, C2 = 1,20 nF.
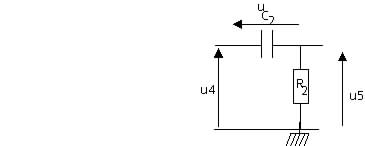
Le chronogramme de la tension u4 considérée est celui qui est dessiné sur la feuille graphique 3. Tous les tracés demandés dans la question B-2 seront réalisés sur cette feuille.
a. A l'instant t = 0-, le condensateur est déchargé. En déduire les valeurs de uC2 et u5.
b. Étude pour 0 < t <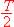 
.
1. A l'instant t = 0+, quelles sont les valeurs de uC2 et u5?
2. Vers quelles valeurs limites les tensions uC2 et u5 tendraient-elles si cet état se prolongeait indéfiniment?
3. Calculer numériquement la constante de temps t du circuit.
4. Calculer le niveau atteint par les tensions uC2 et u5 au bout d'une durée t.
5. A l'instant t =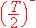 
on donne u5 = 3,52 V; tracer les courbes uC2(t) et u5(t).
c. Étude pour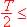 
t < T.
1. A l'instant t =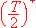 
quelles sont les valeurs de uC2 et u5?
2., 3., 4. mêmes questions qu'en partie B-2 b.
5. A l'instant t = T-, on donne u5 = - 2,28 V; tracer les courbes uC2(t) et u5(t).
6. Le cahier des charges du montage global est-il réalisé?
B-3 Étude du montage précédent avec la diode:
ƒ Compte tenu de la caractéristique de la diode D, représentée ci-dessus, tracer le nouveau chronogramme de la tension u5, sur la feuille graphique 3 en le justifiant.
ƒ En déduire le rôle de la diode dans le montage global.
B-4 Étude de la tension u6:
On donne la caractéristique de transfert en tension de l'opérateur T2:
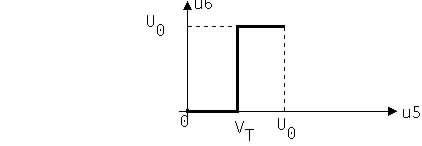
U0 = 10 V; VT = 5 V.
a. En concordance avec le chronogramme de u5 (de la partie B-3), tracer le chronogramme de u6 sur la feuille graphique 3.
b. Sachant que, sur l'intervalle 0 
, la tension u5 est donnée par:
déterminer l'expression littérale de la durée q pendant laquelle la tension u6 est à l'état haut.
Vérifier que q = kC2 ; calculer k en précisant son unité.
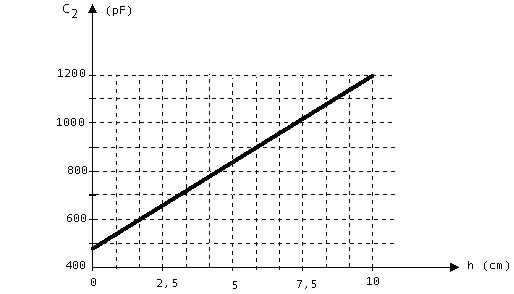
B-5 On donne la relation entre C2 et h sous la forme de graphe:
Exploiter la courbe ci-dessous pour vérifier que la durée q s'exprime en fonction de h par: q = ah + b avec a = 6,32 ms.cm-1 et b = 36,6 ms.
C- ÉTUDE DU FILTRE:
Le schéma du filtre est le suivant:
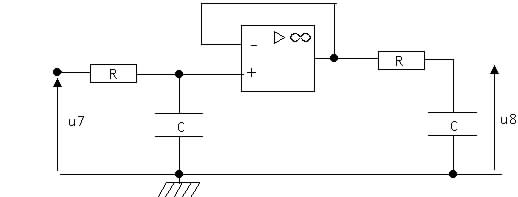
C-1 Étude de l'étage à amplificateur opérationnel:
ƒ Justifier que cet étage peut fonctionner en régime linéaire.
ƒ Quel est alors son rôle?
C-2 Étude du filtre en régime sinusoïdal de fréquence f:
a. En régime linéaire, montrer que la fonction de transfert complexe T de ce filtre peut s'écrire:
b. On désigne par T le module de T.
ƒ Calculer T en fonction de R, C et w.
ƒ En déduire le sens de variation de T en fonction de la fréquence.
ƒ Quel est le type du filtre?
ƒ Déterminer l'expression littérale de la fréquence de coupure à -3dB. Faire l'application numérique.
c. En étudiant les limites de T pour f 
0 et f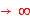 
, donner la plage de variation de F = arg T.
d. La tension sinusoïdale u7 de fréquence f = F = 3,33 kHz et d'amplitude 5 V s'écrit:
u7 = 
La tension u8 est donc de la forme: u8 =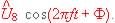 
ƒ Calculer numériquement l'ordre de grandeur de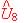 
, et, sachant que l'on considère comme nulle une tension pour laquelle 
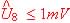, conclure.
C-3 Utilisation du filtre en régime périodique:
La tension u7 qui n'est autre que la tension u6 du convertisseur (partie B) est donnée ci-dessous; sa fréquence F est égale à 3,33 kHz.
La tension peut être approchée par la somme suivante:
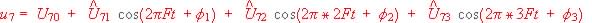
a. En utilisant les résultats précédents avec les valeurs numériques, expliquer pourquoi on peut admettre que u8 est pratiquement une tension continue, de valeur U70, que , que l'on exprimera en fonction de q, T et U0.
b. On rappelle que q = ah + b avec a = 6,32 ms.cm-1 et b = 36,6 ms.
q en ms, h en cm: hauteur du niveau d'acétone.
ƒ Montrer que u8 peut s'écrire: u8 = A.h + B.
ƒ Calculer A et B en précisant les unités.
c. Une variation Dh de la hauteur de niveau d'acétone provoque une variation Du8 de la tension u8 (voir paragraphe B).
ƒ Calculer la sensibilité Sc du conditionneur définie par:
Sc = 
Nom Prénom: .......................................................................................................
Feuille graphique 1: e1(t), s(t) et s(e1)
Feuille graphique 2: u1(t) et u3(t)
Feuille graphique 3
Sans diode:
Avec diode:
