Vous en avez rêvé, eh bien continuez! Voici néanmoins une liste non exhaustive de ce qu'il faut absolument savoir. En partant du principe que le minimum est acquis comme par exemple le calcul sur les impédances, complexes ou non, les amplifications en tensions des montages à aop, transformation de Thévenin Norton
- Structure série à parallèle
- Signaux périodiques
- Modèle équivalent d'un quadripôle
- Filtres
- Comparateurs
- Amplification
- Fonctions mathématiques
- Monostable
- Systèmes commandés
- Oscillateurs sinusoïdaux
- Oscillateurs non sinusoïdaux
- Télécharger le document
(71ko)
- Retour page d'accueil
Passage de la structure série à la structure parallèle: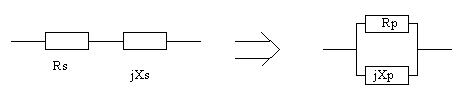
Facteur de qualité:
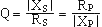
RP = RS ( 1 + Q2 ) et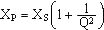 
pour une inductance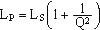 
pour un condensateur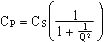 
Signaux périodiques:
- u(t) = < u > + ua(t) composante continue (valeur moyenne) + composante alternative
si < u > = 0 le signal est alternatif.
- Décomposition d'un signal périodique:
u(t) = U0 + U1max cos( 2pft + f1) + U2maxcos(2p(2f)t + f2) + U3maxcos(2p(3f)t + f3) + .....
composante continue(0) + le fondamental (1) + les harmoniques (2,3,4...)
- Valeur moyenne de
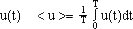
Modèle équivalent d'un quadripôle:
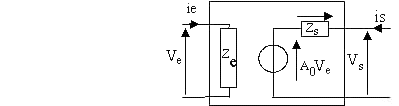
(Voir le modèle du quadripôle aop)
Filtres:
- Bande passante: intervalle de fréquence pour lesquelles G > Gmax - 3dB ou
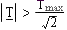
- Transmittance ou fonction de transfert:
passe bas:
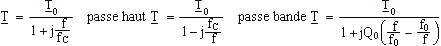
- Filtre passif:la fonction de transfert dépend de la charge, mise en cascade délicate.
- passe-bas:
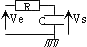Gain max aux faibles fréquences fC = 1/(2pRC), T0 = 1
sert à extraire la composante continue d'un signal (valeur moyenne)
- passe-haut:
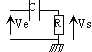Gain max aux hautes fréquences fC = 1/(2pRC), T0= 1
élimine la composante continue ou élimine une fréquence indésirable si f <<fC
- passe-bande:
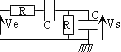filtre à pont de Wien f0 = 1/(2pRC), Q0=T0 = 1/3
sélectionne une bande de fréquence. Si BP étroite le filtre est dit sélectif.
- passe-bas:
- Filtres actif: la fonction de transfert ne dépend pas de la charge, mise en cascade facile.
Réalisation de tous les filtres sans bobines. Inconvénient la BP de l'aop limite la BP du filtre.
- passe-bas:ex R1 , R2C parallèle dans la contre réaction ("C en haut") + de l'aop à la masse.
fC = 1/(2pR2C);
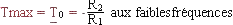
- passe-haut: ex R1C1série, R2 dans la contre réaction. ("C en bas") + de l'aop à la masse.
fC = 1/(2pR1C);
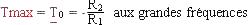
- passe bande: ex R1C1série, R2C2parallèles dans la contre réaction.
ex R1 , RLCparallèle dans la contre réaction.
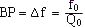
- passe-bas:ex R1 , R2C parallèle dans la contre réaction ("C en haut") + de l'aop à la masse.
Comparateurs à un ou deux seuils:
- Comparateur simple: aop nu VE sur + Vref sur - VS = VSAT si VE > Vref
- Comparateur à hystérésis ou trigger de Schmidtt à aop:
R1 , R2 dans la réaction positive
seuils = valeurs de VE qui font basculer VS
premier seuil obtenu quand la tension différentielle d'entrée s'annule avec VS = VSAT
deuxième seuil quand la tension différentielle d'entrée s'annule avec VS = -VSAT
- Comparateurs à CMOS:
R1 2NAND R2 en réaction des deux NAND
seuils = valeurs de VE qui font basculer VS
premier seuil quand la tension d'entrée de la première porte = VDD/2 avec VS = VDD
deuxième seuil quand la tension d'entrée de la première porte = VDD/2 avec VS = 0
- Applications: production d'un signal rectangulaire à partir d'un signal sinusoïdal ou qcq.
Amplification de différence: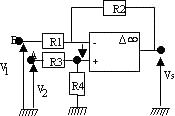 
VS = k (V2 - V1 ) si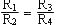 
Si non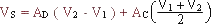 
AD amplification différentielle
AC amplification de mode commun
Application: amplifier une tension non référencée à la masse en sortie d'un capteur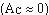 
.
Amplification de puissance:amplifier le courant, la tension est amplifiée par des montages à aop.
- Amplification de classe A:
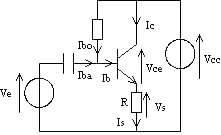Rendement max h = 25 %
- Amplification de classe B: rendement max h = 78 %.
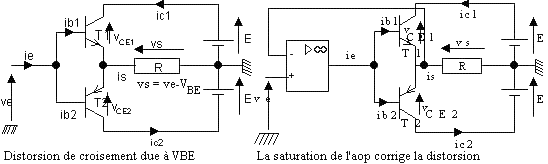
- Idéalisation de l'amplificateur:
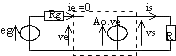
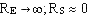
vS = A0 vE ; vS indépendant de R et A0 = AV
Fonctions mathématiques:
- Intégrateur:
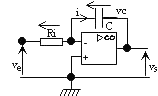Etude Harmonique: filtre passe-bas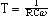 
Etude temporelle:
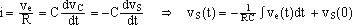
- Dérivateur:
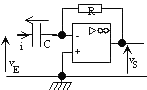Etude harmonique: c'est un filtre passe-haut T = RCw
Etude temporelle:
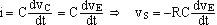
- Multiplieur analogique: vS(t) = k. v1(t).v2(t) avec k en V-1.
Applications: associé à un filtre passe-bas pour la mesure du cosf ou puissance moyenne
P = UIcosf dans un wattmètre.
associé à un filtre passe-haut élever une tension au carré, multiplier f par deux.
Monostable:
- Monostable à aop:
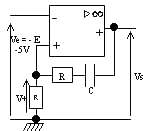
Difficile de généraliser, mais démarche à retenir:
- Etat stable: pas de courant dans R et C; déterminer vS donc vd cad v+ - ve (ici vd >0)
- Impulsion: pour le passage à l'état instable vd doit changer de signe d'où la nature de l'impulsion
(il faut que vd < 0 cad v+ - ve <0 donc ve > v+ . Une impulsion positive de ve déclenche le mono)
- Etat instable: représenter le circuit de charge du condensateur et les sauts de tensions avant et après l'impulsion en retenant que
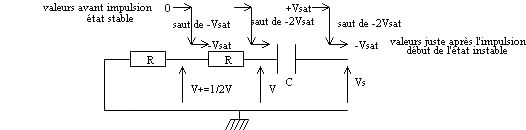
il n'y a pas de discontinuité de tension aux bornes d'un condensateur: vC(0-) = vC(0+) donc même saut de tension pour v que pour vS cad si vS fait un saut de -2VSAT la tension v fait le même saut.
(Evolution: v+ part de -VSAT , et tend vers sa valeur de l'état stable cad 0. quand v+ = -E = -5V on a vd = 0: basculement de vS fin de l'état instable.)
- Durée du monostable: tend mis par v+ pour passer de sa valeur au début de l'état instable
(-VSAT ) à la valeur qui fait basculer vS (-5V) en tendant exponentiellement vers sa valeur à l'état stable (0V). - Formule à ne pas retenir mais si on la retient c'est mieux (merci TI, merci CASIO):
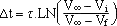
Ici Dt = 2RC.Ln(VSAT/E)
- Etat stable: pas de courant dans R et C; déterminer vS donc vd cad v+ - ve (ici vd >0)
- Monostable à CMOS:
même raisonnement sauf que les états de vS sont 0 et VDD
le changement d'état de vS se fait a VDD/2 pour la tension d'entrée de la première porte.
Systèmes commandés en chaîne fermée: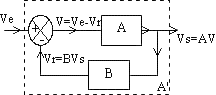
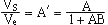
A chaîne d'action, B chaîne de réaction
Application: pour les montages à aop qui sont boublés:
- si la réaction se fait sur l'entrée non inverseuse l'aop fonctionne en saturation
- si la réaction se fait sur l'entrée inverseuse l'aop fonctionne en régime linéaire.
Voir à ce propos: réaction positive et réaction négative de l'aop - Dans le dernier cas l'amplification est fixée par la chaîne de réaction (
- Intérêt: dans le cas d'un aop non bouclé VS = A0.e comme A0 est très grand VS sature.
La réaction permet de fixer l'amplification par des résistances extérieures à l'aop.
Oscillateurs quasi-sinusoïdaux: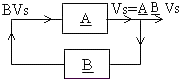
donc A B = 1
Solution: A.B = 1 et arg(A) + arg(B) = 0
Si A est réel alors B aussi. Le bloc B est un circuit sélectif.
B est réel pour f0 fréquence des oscillations.
- Oscillateur à pont de Wien:
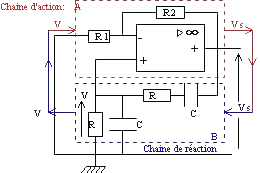
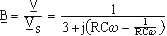
Condition d'oscillations: B réel donc Arg(B) = 0
comme A B = 1 on a A = 3.
La boucle de réaction réintroduit la tension de sortie en la divisant par 3.
La boucle d'action doit compenser et multiplier la tension d'entrée par 3.
Conclusion: le gain de l'amplificateur compense les pertes introduites par la chaîne de retour.
- Oscillateur à résistance négative:
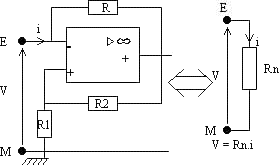
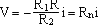
Application: placée dans un circuit RLC si ½Rn½= R on obtient des oscillations sans amortissement.
Le système a des limites: la saturation de l'aop.
Oscillateurs non sinusoïdaux:
- Astable à aop:
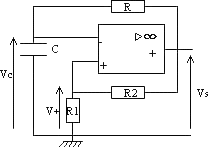
L'aop R1 et R2 constituent un comparateur à hystérésis. vS peut prendre 2 valeurs +VSAT ou -VSAT.
Quand vS = +VSAT , C se charge à travers R jusqu'à ce que vd change de signe alors
vS = - VSAT et C se décharge à travers R jusqu'à ce que vd change de signe ....
Les changement de signe de vd se font quand vC = VH et vC = VB seuils du trigger.
- Circuit de charge de C:
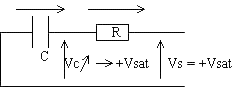vC croît de VB et tend vers +VSAT
- Période de l'astable: T = tHAUT + tBAS
Durée de l'état haut: temps mis par vC pour passer de VB à VH en tendant vers +VSAT
Durée de l'état bas: temps mis par vC pour passer de VH à VB en tendant vers -VSAT
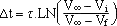
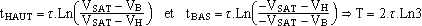
- Circuit de charge de C:
- Astable à CMOS:
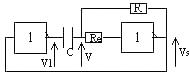vS = 0 ou VDD et seuil de basculement VDD/2
Quand vS = VDD v1 = 0 et C se charge à travers R v tend vers vDD (faire le circuit de charge) mais stop à VDD/2
quand vS = 0 v1 = VDD et C se décharge à travers R. v tend vers 0 et s'arrête à VDD/2.